Uma reta r não-vertical, de coeficiente angular m, que passa pelo ponto A(xA, yA). Vamos obter a equação dessa reta, tomando um ponto P(x, y) tal que P ≠ A.
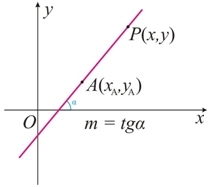
A equação fundamenta da reta é:

Equação geral da reta
Toda reta r do plano cartesiano pode ser expressa por uma equação do tipo:

Em que:
• a, b, e c são números reais;
• a e b não são simultaneamente nulos.
Podemos obter a equação geral de uma reta r conhecendo dois pontos não coincidentes de r:

Para isso, usa-se a condição de alinhamento de A e B com um ponto genérico P(x,y) de r.
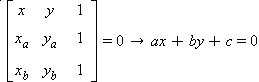
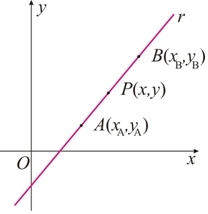
Equação reduzida da reta
Vamos determinar a equação da reta r que passa por Q(0,q), e tem coeficiente angular m = tg(α):

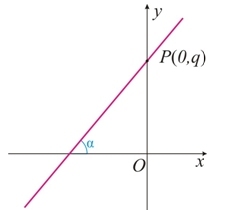
Toda equação na forma y = mx + q é chamada equação reduzida da reta, em que m é o coeficiente angular e q a ordenada do ponto n qual a reta cruza o eixo Oy. A equação reduzida pode ser obtida diretamente da equação geral ax + by + c = 0:

Onde:

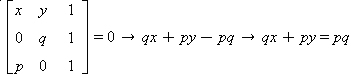
Vamos determinar a equação da reta r que passa por Q(0,q), e tem coeficiente angular m = tg(α):


Toda equação na forma y = mx + q é chamada equação reduzida da reta, em que m é o coeficiente angular e q a ordenada do ponto n qual a reta cruza o eixo Oy. A equação reduzida pode ser obtida diretamente da equação geral ax + by + c = 0:

Onde:

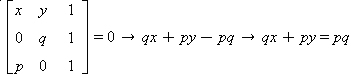
Equação segmentária da reta
Considere uma reta r que cruza os eixos cartesianos nos pontos (0, q) e (p, 0).
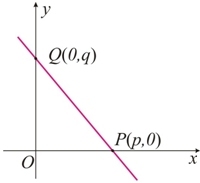
Vamos escrever a equação da reta r:
Dividindo essa equação por pq, obtemos a equação segmentária da reta:

Link: http://www.infoescola.com/geometria-analitica/equacoes-da-reta/
Considere uma reta r que cruza os eixos cartesianos nos pontos (0, q) e (p, 0).

Vamos escrever a equação da reta r:
Dividindo essa equação por pq, obtemos a equação segmentária da reta:

Link: http://www.infoescola.com/geometria-analitica/equacoes-da-reta/
Nenhum comentário:
Postar um comentário