Exercício sobre Coeficiente Angular
sábado, 21 de dezembro de 2013
quarta-feira, 18 de dezembro de 2013
Geometria Plana - ENEM - 2012 ( Matemática )
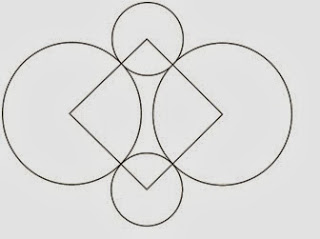
O losango representado na Figura 1 foi formado pela união dos centros das quatro circunferências tangentes, de raios de mesma medida
Figura 1
Dobrando-se o raio de duas das circunferências centradas em vértices opostos do losango e ainda mantendo- -se a configuração das tangências, obtém-se uma situação conforme ilustrada pela Figura 2.
Figura 2
O perímetro do losango da Figura 2, quando comparado ao perímetro do losango da Figura 1, teve um aumento de
A) 300%
B) 200%
C) 150%
D) 100%
E) 50%
Gabarito: E
Disponível em: http://www.profcardy.com/exercicios/assunto.php?assunto=Geometria%20Plana acesso em 18/12/13
Geometria Plana

Princípios básicos de Geometria Plana.
Os estudos iniciais sobre Geometria Plana estão relacionados à Grécia Antiga, também pode ser denominada Geometria Euclidiana em homenagem a Euclides de Alexandria (360 a.C. - 295 a.C.), grande matemático educado na cidade de Atenas e frequentador da escola fundamentada nos princípios de Platão.
Os princípios que levaram à elaboração da Geometria Euclidiana eram baseados nos estudos do ponto, da reta e do plano. O ponto era considerado um elemento que não tinha definição plausível, a reta era definida como uma sequência infinita de pontos e o plano definido através da disposição de retas.
As definições teóricas da Geometria de Euclides estão baseadas em axiomas, postulados, definições e teoremas que estruturam a construção de variadas formas planas. Os polígonos são representações planas que possuem definições, propriedades e elementos.
Podemos relacionar à Geometria plana os seguintes conteúdos programáticos:
Ponto, reta e plano
Posições relativas entre retas
Ângulos
Triângulos
Quadriláteros
Polígonos
Perímetro
Áreas de regiões planas
Disponível em: http://www.brasilescola.com/matematica/geometria-plana.htm acesso em 18/12/13
Área de uma Região Triangular
A área de uma região triangular é dada pela seguinte fórmula:

h = medida da altura
b = medida da base
Podemos escrever: a área de uma região triangular é dada pela metade do produto da medida base pela medida da altura correspondente.
Exemplo 1
.jpg)
Nem sempre podemos usar a fórmula citada anteriormente, pois em algumas situações a base ou a altura não são dadas, tendo então que recorrer à Fórmula de Heron.
Dado um triângulo de lados a, b e c temos:
Onde p é o valor do semiperímetro.
Exemplo 2
.jpg)
Há outra forma de calcular a área de um triângulo, quando conhecemos as medidas de dois de seus lados e a medida do ângulo formado por eles, a área da região será calculada da seguinte forma:
Exemplo 3
.jpg)
Exemplo 3
.jpg)
Disponível em: http://www.brasilescola.com/matematica/area-do-triangulo.htm acesso em 18/12/13
Ângulo formado entre duas retas
Considere duas retas distintas e concorrentes do plano, r e s, ambas oblíquas aos eixos coordenados e não perpendiculares entre si. As duas retas formam um ângulo entre si, que denominaremos de α. Esse ângulo α é tal que:
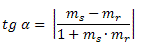
Onde ms e mr são os coeficientes angulares das retas s e r, respectivamente.
Se ocorrer de uma das retas ser vertical e a outra oblíqua, o ângulo α formado entre elas é tal que:
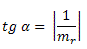
Exemplo 1. Determine o ângulo formado entre as retas r: x - y = 0 e s: 3x + 4y – 12 =0
Solução: Para determinar o ângulo formado entre as duas retas, precisamos conhecer o coeficiente angular de cada uma delas. Assim, vamos determinar o coeficiente angular das retas r e s.
Para a reta r, temos:
x - y = 0
y = x
Portanto, mr = 1.
Para a reta s, temos:
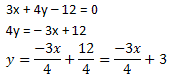
Portanto, ms = -3/4
Conhecendo os valores dos coeficientes angulares, basta aplicar a fórmula do ângulo entre duas retas:
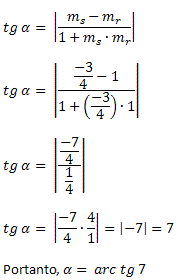
Exemplo 2. Determine o ângulo formado entre as retas r: y = 3x + 4 e s: y = – 2x + 8.
Solução: Vamos determinar o coeficiente angular de cada uma das retas dadas.
Para a reta r, temos:
y = 3x + 4
mr = 3
Para a reta s, temos:
y = – 2x + 8
ms = – 2
Aplicando a fórmula do ângulo entre duas retas, obtemos:
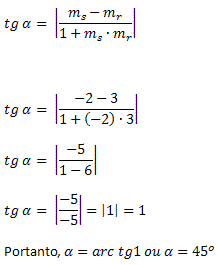
Disponível em: http://www.mundoeducacao.com/matematica/angulo-formado-entre-duas-retas.htm acesso em 18/12/13
Distância entre ponto e reta
A distância entre um ponto e uma reta é calculada unindo o próprio ponto à reta através de um segmento, que deverá formar com a reta um ângulo reto (90º). Para estabelecer a distância entre os dois necessitamos da equação geral da reta e da coordenada do ponto. A figura a seguir estabelece a condição gráfica da distância entre o ponto P e a reta r, sendo o segmento PQ a distância entre eles.
.jpg)
Estabelecendo a equação geral da reta s: ax0 + by0 + c = 0 e a coordenada do ponto P(x0,y0), conseguimos chegar à expressão capaz de calcular a distância entre o ponto P e a reta s:
.jpg)
Essa expressão surge de uma generalização feita, podendo ser utilizada nas situações em que envolve o cálculo da distância entre um ponto qualquer e uma reta.
Exemplo
Dado o ponto A(3, -6) e r: 4x + 6y + 2 = 0. Estabeleça a distância entre A e r utilizando a expressão dada anteriormente.
Temos que:
x: 3
y: -6
a: 4
b: 6
c: 2
.jpg)
Exercícios:
1. Encontre a equação da reta s, perpendicular à reta t: 2x + 3y – 4 =0, sabendo que ela passa pelo ponto P(3,4).
Solução
.gif)
2. Considere no plano cartesiano uma reta r de equação 3x + 5y +1 =0 e um ponto Q de coordenadas (5,5). Determine a equação da resta s perpendicular a r passando por Q.
Solução
.gif)
Disponível em: http://exercicios.brasilescola.com/matematica/exercicios-sobre-retas-perpendiculares.htm#resposta-2407 acesso em 18/12/13
Retas perpendiculares
A característica mais conhecida de duas retas perpendiculares é que no ponto de intersecção delas é formado um ângulo reto (de medida igual a 90°), mas com o estudo da geometria analítica em cima da análise da reta é possível dizer que duas retas perpendiculares terão os seus coeficientes angulares opostos e inversos.
Considere duas retas r e s, perpendiculares no ponto C, representadas em um plano cartesiano.
Considerando o ângulo de inclinação da reta s como sendo β, então o ângulo de inclinação da reta r será 90° - β. Dessa forma teremos:
Coeficiente angular da reta s: ms = tg β
Coeficiente angular da reta r: mr = tg (90° - β)
.jpg)
Aplicando as fórmulas de adição de arcos é possível comparar o coeficiente angular das duas retas, veja:
tg (90° + β) = sen (90° + β) = sen90° . cos β + sen β . cos β
cos (90° + β) cos90° . cos β – sen 90° . sen β
tg (90° + β) = cos β
-sen β
tg (90° + β) = - 1
tg β
cos (90° + β) cos90° . cos β – sen 90° . sen β
tg (90° + β) = cos β
-sen β
tg (90° + β) = - 1
tg β
Como ms = tg β e mr = - 1 / tg β, podemos dizer que:
ms = -1 / mr ou ms . mr = -1
ms = -1 / mr ou ms . mr = -1
Dessa forma, chegamos à conclusão de que em duas retas perpendiculares o coeficiente angular de uma das retas será igual ao oposto do inverso do coeficiente angular da outra.
Disponível em: http://www.brasilescola.com/matematica/retas-perpendiculares.htm acesso em 18/12/13
Intercessão entre retas:
A interseção é um
ponto comum entre as retas.
O
Exemplo: As equações gerais das duas retas r e s são respectivamente, x + 4y – 7 = 0 e 3x + y + 1 = 0. Determine o ponto P(x0, y0) comum às retas r e s.
Sabemos que o ponto de intersecção de duas retas concorrentes é a solução do sistema formado por elas. Assim, veja a resolução do sistema abaixo:
x + 4y – 7 = 0
3x + y + 1 = 0
x + 4y = 7 (-3)
3x + y = -1
-3x – 12y = -21
3x + y = -1
-11y = -22
y = 2
Substituindo o valor de y em qualquer uma das equações iremos obter o valor de
x:
x + 4y = 7
x + 4 . 2 = 7
x + 8 = 7
x = 7 – 8
x = -1
x + 4y = 7
x + 4 . 2 = 7
x + 8 = 7
x = 7 – 8
x = -1
Portanto, o ponto P(x0, y0) = (-1,2).
No início da explicação foi dito que as retas t: atx + bty + ct = 0 e u: aux + buy + cu = 0 são concorrentes. Para que seja verdadeira essa afirmação o sistema formado por elas deverá ser possível e determinado, essa verificação irá funcionar da seguinte forma:
atx + bty + ct = 0
aux + buy + cu = 0
atx + bty = - ct
aux + buy = - cu
E para que esse sistema seja possível e determinado, o seu determinante deverá ser diferente de zero.
No início da explicação foi dito que as retas t: atx + bty + ct = 0 e u: aux + buy + cu = 0 são concorrentes. Para que seja verdadeira essa afirmação o sistema formado por elas deverá ser possível e determinado, essa verificação irá funcionar da seguinte forma:
atx + bty + ct = 0
aux + buy + cu = 0
atx + bty = - ct
aux + buy = - cu
E para que esse sistema seja possível e determinado, o seu determinante deverá ser diferente de zero.
Exemplo:
Resolve o sistema de equações e determine o x e y, que dá o ponto de interseção.
Se o sistema for determinado, elas não são paralelas.
2x - y = 4
6x - 2y =10
Multiplica a primeira por -2 e soma as duas:
-4x + 2y = -8
6x - 2y =10
---------------------
2x = 2
x = 1
Substitui x na primeira:
2x-y= 4
2 - y = 4
y = -2
O ponto de intersecção é (1,-2) e isso mostra que não são paralelas.
Verifique se as retas 2x + y – 3
= 0 e 6x + 5y + 1 = 0 são concorrentes.
2x + y = 3
6x + 5y = -1

2 . 5 – (1 . 6) ≠ 0
10 – 6 ≠ 0
4 ≠ 0
2x + y = 3
6x + 5y = -1

2 . 5 – (1 . 6) ≠ 0
10 – 6 ≠ 0
4 ≠ 0
Exercício:
Resolve o sistema de equações e determine o x e y, que dá o ponto de interseção.
Se o sistema for determinado, elas não são paralelas.
2x - y = 4
6x - 2y =10
Multiplica a primeira por -2 e soma as duas:
-4x + 2y = -8
6x - 2y =10
---------------------
2x = 2
x = 1
Substitui x na primeira:
2x-y= 4
2 - y = 4
y = -2
O ponto de intersecção é (1,-2) e isso mostra que não são paralelas.
Disponível em: http://professoradanielamendes.blogspot.com.br/2010/06/como-eu-acho-o-ponto-de-interseo-entre.html acesso em 18/12/13
Exercícios:
1- Dadas
as retas r : 3x + 2y - 15 = 0 ; s : 9x + 6y - 45 = 0 e t : 12x + 8y - 60 = 0 ,
podemos afirmar:
a) elas são paralelas
b) elas são concorrentes
c) r Ç t Ç s = R
d) r Ç s Ç t = R2
e) as três equações representam uma mesma reta .
Solução:
Primeiro vamos verificar as retas r e s: 3 / 9 = 2 / 6 = -15 / -45 (primeiro caso acima) e portanto as
retas r e s são coincidentes.
Comparando agora, por exemplo a reta r com a reta t , teremos:
3 / 12 = 2 / 8 = -15 / -60 (primeiro caso acima);
Portanto as retas r, s e t são coincidentes, ou seja, representam a mesma reta.
Logo a alternativa correta é a letra E.
Disponível em: http://pir2.forumeiros.com/t6570-geom-analitica-posicao-relativa-de-duas-retas acesso em 18/12/13
Posições relativas de duas retas no plano
Retas paralelas
Duas retas são paralelas se não tiverem nenhum ponto em comum ou todos em comum e seus coeficientes angulares forem iguais ou não existirem.
Duas retas são paralelas se não tiverem nenhum ponto em comum ou todos em comum e seus coeficientes angulares forem iguais ou não existirem.
As retas u e t são paralelas e distintas. E por serem perpendiculares ao eixo Ox os seus coeficientes angulares não irão existir.
As retas u e t são paralelas e coincidentes, pois possuem todos os pontos em comum. E por serem perpendiculares ao eixo Ox os seus coeficientes angulares não irão existir.
As retas u e t são paralelas e distintas. E os seus coeficientes angulares serão iguais.
As retas u e t são paralelas e coincidentes, pois possuem todos os pontos em comum. E os seus coeficientes angulares serão iguais.
Retas concorrentes
Duas retas são concorrentes se possuírem apenas um ponto em comum. E seus coeficientes angulares poderão ser diferentes ou um existir e o outro não.
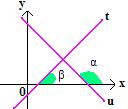
As retas u e t são coincidentes e as inclinações das retas são diferentes de 90°. Assim, seus coeficientes angulares serão diferentes.
.jpg)
As retas u e t são concorrentes e a inclinação da reta t é de 90°, sendo assim seu coeficiente angular não irá existir, mas o coeficiente da reta u existe, pois não é perpendicular ao eixo Ox.
Retas concorrentes
Duas retas são concorrentes se possuírem apenas um ponto em comum. E seus coeficientes angulares poderão ser diferentes ou um existir e o outro não.
As retas u e t são coincidentes e as inclinações das retas são diferentes de 90°. Assim, seus coeficientes angulares serão diferentes.
.jpg)
As retas u e t são concorrentes e a inclinação da reta t é de 90°, sendo assim seu coeficiente angular não irá existir, mas o coeficiente da reta u existe, pois não é perpendicular ao eixo Ox.
Disponível em: http://www.mundoeducacao.com/matematica/posicoes-relativas-duas-retas.htm acesso em 18/12/13
Exercício de fixação
Exercício 4: (UFSC 2011)
A reta que passa pela origem e pelo ponto médio do segmento AB com A=(0,3) e B=(5,0) tem qual coeficiente angular?
A)

B)

C)

D)

Resposta (a)
Link dos exercícios: http://www.infoescola.com/geometria-analitica/equacoes-da-reta/exercicios/
Link dos exercícios: http://www.infoescola.com/geometria-analitica/equacoes-da-reta/exercicios/
Mais exercícios :3
Exercício 2: (UDESC 2008)
A soma do coeficiente angular com o coeficiente linear da reta que passa pelos pontos A(1, 5) e B(4, 14) é:
A) 4
B) -5
C) 3
D) 2
E) 5
Resposta (e)
Exercícios ;)
Exercício 1: (ADVISE 2009)
A equação geral da reta tangente à curva y = x² + x no ponto de abscissa 1 é:
A) 3x – y – 1 = 0
B) 3x – y = 0
C) 2x – y – 1 = 0
D) 2x – y = 0
E) 5x – 2y – 2 = 0
Resposta (a)
Formas de equação na reta
Uma reta r não-vertical, de coeficiente angular m, que passa pelo ponto A(xA, yA). Vamos obter a equação dessa reta, tomando um ponto P(x, y) tal que P ≠ A.
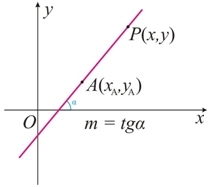
A equação fundamenta da reta é:

Equação geral da reta
Toda reta r do plano cartesiano pode ser expressa por uma equação do tipo:

Em que:
• a, b, e c são números reais;
• a e b não são simultaneamente nulos.
Podemos obter a equação geral de uma reta r conhecendo dois pontos não coincidentes de r:

Para isso, usa-se a condição de alinhamento de A e B com um ponto genérico P(x,y) de r.
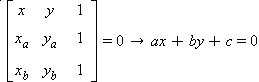
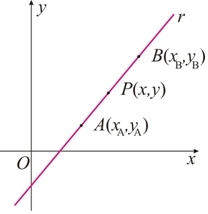
Equação reduzida da reta
Vamos determinar a equação da reta r que passa por Q(0,q), e tem coeficiente angular m = tg(α):

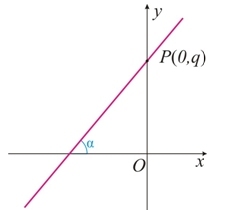
Toda equação na forma y = mx + q é chamada equação reduzida da reta, em que m é o coeficiente angular e q a ordenada do ponto n qual a reta cruza o eixo Oy. A equação reduzida pode ser obtida diretamente da equação geral ax + by + c = 0:

Onde:

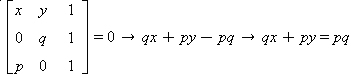
Vamos determinar a equação da reta r que passa por Q(0,q), e tem coeficiente angular m = tg(α):


Toda equação na forma y = mx + q é chamada equação reduzida da reta, em que m é o coeficiente angular e q a ordenada do ponto n qual a reta cruza o eixo Oy. A equação reduzida pode ser obtida diretamente da equação geral ax + by + c = 0:

Onde:

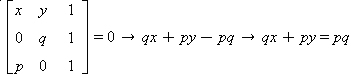
Equação segmentária da reta
Considere uma reta r que cruza os eixos cartesianos nos pontos (0, q) e (p, 0).
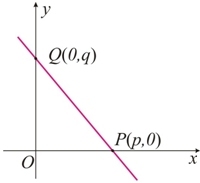
Vamos escrever a equação da reta r:
Dividindo essa equação por pq, obtemos a equação segmentária da reta:

Link: http://www.infoescola.com/geometria-analitica/equacoes-da-reta/
Considere uma reta r que cruza os eixos cartesianos nos pontos (0, q) e (p, 0).

Vamos escrever a equação da reta r:
Dividindo essa equação por pq, obtemos a equação segmentária da reta:

Link: http://www.infoescola.com/geometria-analitica/equacoes-da-reta/
Equação da reta conhecendo m e um ponto
Queridos, segue um link explicativo sobre o assunto ;)
http://www.youtube.com/watch?v=X8g5SFm29tA
segunda-feira, 16 de dezembro de 2013
Cálculo do coeficiente angular de uma reta

Aplicando:
Exemplo 1
Qual é o coeficiente angular da reta que passa pelos pontos A (–1,3) e B (–2,4)?
m = Δy/Δx
Exemplo 2
O coeficiente angular da reta que passa pelos pontos A (2,6) e B (4,14) é:
m = Δy/Δx
Exemplo 3
O coeficiente angular da reta que passa pelos pontos A (8,1) e B (9,6) é:
m = Δy/Δx
Disponível em: http://www.brasilescola.com/matematica/calculo-coeficiente-angular-uma-reta.htm acesso em 16/12/13.
Assinar:
Comentários (Atom)