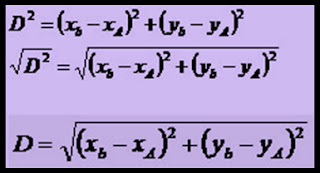- Condições de alinhamento de três pontos:

Três pontos não alinhados em um plano cartesiano formam um triângulo de vértices A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C). A sua área poderá ser calculada da seguinte forma:

A = 1/2 . |D|, ou seja, |D| / 2, considerando D = .  



  Para que exista a área do triângulo esse determinante deverá ser diferente de zero. Caso seja igual a zero os três pontos, que eram os vértices do triângulo, só poderão estar alinhados.

   Portanto, podemos concluir que três pontos distintos A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C) estarão alinhados se


 o determinante correspondente a eles  for igual a zero.

                                 

Exercício:

Verifique se os pontos A(0,5), B(1,3) e C(2,1) são ou não colineares (são alinhados).

O determinante referente a esses pontos é    . Para que sejam colineares, o valor desse determinante deve ser igual à zero. 

= 10 + 1 – 6 – 5 = 9 – 6 – 5 = 5 – 5 = 0 

Portanto, os pontos A, B e C estão alinhados.

Disponível em: http://www.brasilescola.com/matematica/condicao-alinhamento-tres-pontos-utilizando-determinantes.htm acesso em 25/11/13                                 

Exercício sobre ponto médio:

Determine as coordenadas do ponto médio do segmento AB de extremos A(1, 9) e B(7, 5).



Solução: Temos que

Portanto, o ponto médio do segmento AB tem coordenadas M(4 , 7)

Disponível em: http://www.alunosonline.com.br/matematica/ponto-medio-um-segmento-no-plano.html acesso em 24/11/13.

- Sistema cartesiano ortogonal:

  Se duas retas se cruzam e formam um ângulo de 90º elas são perpendiculares. A perpendicularidade dessas duas retas forma um sistema cartesiano ortogonal.

-Coordenadas do ponto médio:

O segmento de reta possui inúmeros pontos alinhados, mas somente um deles irá dividir o segmento em duas partes iguais. A identificação e a determinação do ponto médio de um segmento de reta será demonstrado com base na ilustração a seguir.

Vamos determinar as coordenadas do ponto médio do segmento PQ da figura.

Assim, o ponto médio tem coordenadas:

Disponível em: http://www.alunosonline.com.br/matematica/ponto-medio-um-segmento-no-plano.html acesso em 24/11/13

Geometria analítica:

4° Unidade

   A Geometria Analítica, também denominada de coordenadas geométricas, se baseia nos estudos da Geometria através da utilização da Álgebra.
  Os estudos relacionados à Geometria Analítica datam seu início no século XVII, Descartes, ao relacionar a Álgebra com a Geometria, criou princípios matemáticos capazes de analisar por métodos geométricos as propriedades do ponto, da reta e da circunferência, determinando distâncias entre eles, localização e pontos de coordenadas.
  Uma característica importante da G.A. se apresenta na definição de formas geométricas de modo numérico, extraindo dados informativos da representação. Com base nesses estudos, a Matemática passa a ser vista como uma disciplina moderna, capaz de explicar e demonstrar situações relacionadas ao espaço.      As noções intuitivas de vetores começam a ser exploradas de forma contundente, na busca por resultados numéricos que expressem as ideias da união da Geometria com a Álgebra.

Disponível em: http://www.brasilescola.com/matematica/geometria-analitica.htm. Acesso em 24/11/13

Questões sobre Geometria Analítica- Vídeo

Como encontrar o valor de y na distancia entre dois pontos?

Questões sobre Geometria Analítica- Vídeo

Como calcular a distancia entre dois pontos?

Questões sobre Estatística - Vídeo

Como calcular média, variância e desvio padrão?

Questões sobre Estatística - Vídeo

Como calcular a média aritmética e ponderada,  e a moda?

Questões sobre Estatística - Vídeo

Como calcular média, mediana e moda na tabela de

Frequência? 

Questões sobre Estatística - Vídeo

Como calcular média, mediana e moda na tabela de 
classe?

Questões sobre Estatística - Vídeo

Tabela com frequência relativa e absoluta.

Vídeo - Questões sobre Estatística

Vídeo Mundo da Estatística

3M15

1 - Calcule a distância entre os pontos:

a) (0, 4) e (0, -3)

d = √(0-0)²+(4-(-3))²
d = √7²
d = √49
d = 7 uc
b) (2, 1) e (1, 5)

d = √(2-1)²+(1-5)²
d = √1²+(-4)²
d = √1+16
d = √17 uc




2 - (UFF) Determine o(s) valor(es) que r deve assumir para que o ponto (r,2) diste cinco unidades do ponto (0,-2).


Se a distância entre os pontos deve ser 5, d = 5:
√(r-0)²+(2-(-2))² = 5
√r²+16 = 5
Para sumir com a raiz, elevamos os dois lados da equação ao quadrado:

(√r²+16)² = 5²
r²+16 = 25
r² = 25-16

r² = 9
r = ± 3
Resposta: -3 ou 3, qualquer um dos dois valores faz os dois pontos terem 5 unidades de distância.

Disponível em: http://www.matematicaemexercicios.com/aulas/geometria-analitica/geometria-analitica.html acesso em 11/11/13

Questão sobre Gráfico Estatístico

Com base no gráfico, pode-se afirmar que:

a) em 1970 a população urbana era menor que a população rural.

b) nos anos considerados, a população rural se manteve praticamente estável.

c) em 1980 a população urbana era cerca de três vezes

a população rural.

d) nos anos considerados, a população urbana aumentou em cerca de 50 milhões a cada ano.

e) nos anos considerados, a população urbana se manteve constante.

Disponível em: http://www.pensevestibular.com.br/enem/exercicios-do-enem-competencia-7 acesso em 11/11/13.

Questões Resolvidas

Depois de jogar um dado em forma de cubo e de faces numeradas de 1 a 6, por 10 vezes consecutivas, e anotar o numero obtido em cada jogada, construiu-se a seguinte tabela de distribuição de frequências. A media, mediana e moda dessa distribuição de frequências são, respectivamente:
a) 3, 2 e 1

b) 3, 3 e 1
c) 3, 4 e 2

d) 5, 4 e 2
e) 6, 2 e 4

Disponível em http://www.pensevestibular.com.br/enem/exercicios-do-enem-competencia-7 acesso em 11/11/13

Questões Resolvidas

Preocupada com a sua locadora, Marla aplicou uma pesquisa com um grupo de 200 clientes escolhidos de forma aleatória, sobre a quantidade de filmes que estes locaram no primeiro semestre de 2011. Os dados coletados estão apresentados na tabela a seguir:

Número de filmes alugados
Número de filmes	Frequência
0	25
1	30
2	55
3	90
Total	200

A média, a moda e a mediana destes dados são, respectivamente, os seguintes:

a) 2,05; 3; 2

b) 1,5; 2; 3

c) 1,5; 3; 3

d) 1,5; 3; 2

e) 2,05; 2; 3

Disponível em http://www.pensevestibular.com.br/enem/exercicios-de-estatistica acesso em 11/11/13

Questões do Enem

ENEM 2011 - Questão 154 – Prova Azul.

A participação dos estudantes na Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP) aumenta a cada ano. O quadro indica o percentual de medalhistas de ouro, por região, nas edições da OBMEP de 2005 a 2009:

Em relação às edições de 2005 a 2009 da OBMEP, qual o percentual médio de medalhistas de ouro da região Nordeste?

A) 14,6%

B) 18,2%

C) 18,4%

D) 19,0%

E) 21,0%

Resoluçao

Disponível em http://soumaisenem.com.br/matematica/conhecimentos-de-estatistica-e-probabilidade/analise-de-tabelas-questoes-do-enem acesso em 11/11/13.

Vídeo explicativo para vocês :)

Olá queridos, hoje inovamos, e trouxemos a solução de uma questão em vídeo pra vocês. Espero que compreendam rs'
Caso tenham alguma questão, e não saibam como resolver, posta aqui no blog. Quem sabe não podemos ajudar vocês.
Beijos, mais tarde tem mais vídeo. ;)

Resposta do exercício PRATICAR !

Questão do Enem 2013

Resolução 

Disnponível em: http://guiadoestudante.abril.com.br/vestibular-enem/enem-2013-correcao-questao-162-matematica-758466.shtml acesso em 01/11/13

Aplicação - Distância entre dois pontos

Exemplo 1

Dados os pontos A (2,-3) e B (4,5), determine a distância entre eles.

xa: 2
xb: 4
ya: -3
yb: 5

Exemplo 2

Calcule a distância entre os pontos P(-2,3) e Q(-5,-9).

xa: -2
xb: -5
ya: 3
yb: -9 

Disponível em http://www.mundoeducacao.com/matematica/distancia-entre-dois-pontos.htm acesso em 01/11/13
 

Distância entre dois pontos

Os estudos em Geometria Analítica possibilitam a relação entre a Álgebra e a Geometria, abrangendo situações em que são envolvidos ponto, reta e figuras espaciais. Um conceito básico de Geometria deve ser aproveitado na GA, a fim de estabelecer a distância entre dois pontos: “por dois pontos passa apenas uma reta”.

Dado o plano cartesiano, vamos estabelecer a distância entre os pontos A e B.

Podemos calcular a distância entre dois pontos com a seguinte fórmula: 

Disponível em http://www.mundoeducacao.com/matematica/distancia-entre-dois-pontos.htm acesso em 01/10/13.

Praticar:

01) Determinar a media, mediana, moda dos seguintes conjuntos de valores:

a)  2,3    2,1   1,5    1,9 

     3,0    1,7    1,2    2,1 

     2,5    1,3    2,0    2,7 

     0,8    2,3    2,1    1,7

b) 37    38     33      42      35

     44    36     28      37      35

     33    40     36      35      37

2) Calcule a média aritmética simples em cada um dos seguintes casos:

a) 15 ; 48 ; 36

b) 80 ; 71 ; 95 ; 100

c) 59 ; 84 ; 37 ; 62 ; 10

d)  1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9

e) 18 ; 25 ; 32

f) 91 ; 37 ; 84 ; 62 ; 50



3) Demonstre através de cálculos a posição da mediana nos dados informados:

           a)    54, 74, 21, 01,12, 33, 03, 76, 40, 56, 89, 102, 04

           b)    87, 45, 12, 120, 107, 05, 34, 02, 09, 01, 19, 29, 22, 17

           c)    25, 74, 65, 12, 33, 03, 76, 40, 56

           d)    45, 12, 100, 05, 34, 02, 09, 19, 29, 01

 Disponível em: www.matematiques.com.br acesso em 01/11/13   

Aplicação

1. Conhecem-se as seguintes idades (em anos) de todos os 6 gorilas do zoo da cidade:

9,1,16,11,10,14

Qual é a média de idades dos gorilas do zoo? Qual é a variância? E o desvio padrão?

Variância:

Desvio Padrão: 

    Nada mais é do que a raiz quadrada do valor da variância, que neste caso é  aproximadamente 4,7.

Referência

Disponível em: http://i9ensino.com/estatistica-media-da-populacao-e-variancia-da-populacao-exercicio-resolvido/ acesso em 01/11/13.